Phalanx: Hardware-Aligned Sliding-Window Recurrences

Read more: Technical report, Kernel library

Introduction

We introduce Phalanx, a layer tailored to modern AI workloads using fast sliding window recurrences (SWR), serving as a faster drop-in replacement for sliding window attention (SWA) . Using our custom block-two-pass (B2P) algorithm and kernel, Phalanx achieves the highest throughput across sequence lengths from 32 to 512K compared to highly optimized attention, local attention, and linear attention variants. Phalanx hybrid models match attention and sliding window attention hybrid baselines in model quality while delivering faster training end-to-end.

Most AI model architectures are designed in theory first and only later implemented to run on GPUs. The result is a mismatch: algorithms that look efficient on paper but stumble on hardware. Our approach flips that design order. Phalanx is a hardware-native layer designed from the ground up to limit communication only to neighboring data, at the fastest level of the memory hierarchy.

Operator	Complexity	Logical Depth	Exploits Locality	Forward time (ms, H100, 8k)
Attention	$O(n^2)$	$O(1)$	No	0.67
SWA	$O(n)$	$O(1)$	Yes	0.36
Recurrent-type (GLA, Mamba, DeltaNet)	$O(n)$	$O(log(n))$	No	0.57
SWR (Phalanx)	$O(n)$	$O(1)$	Yes	0.20

Phalanx

Phalanx is a new type of efficient, local layer for language modeling. Phalanx acts as the local specialist: it handles near-field dependencies through a windowed recurrence while delegating long-range modeling to attention or other mixers. Unlike other recurrence-based layers such as DeltaNet [7], GLA [8], or Mamba [9], Phalanx maintains constant logical depth, making it the fastest layer at any sequence length.

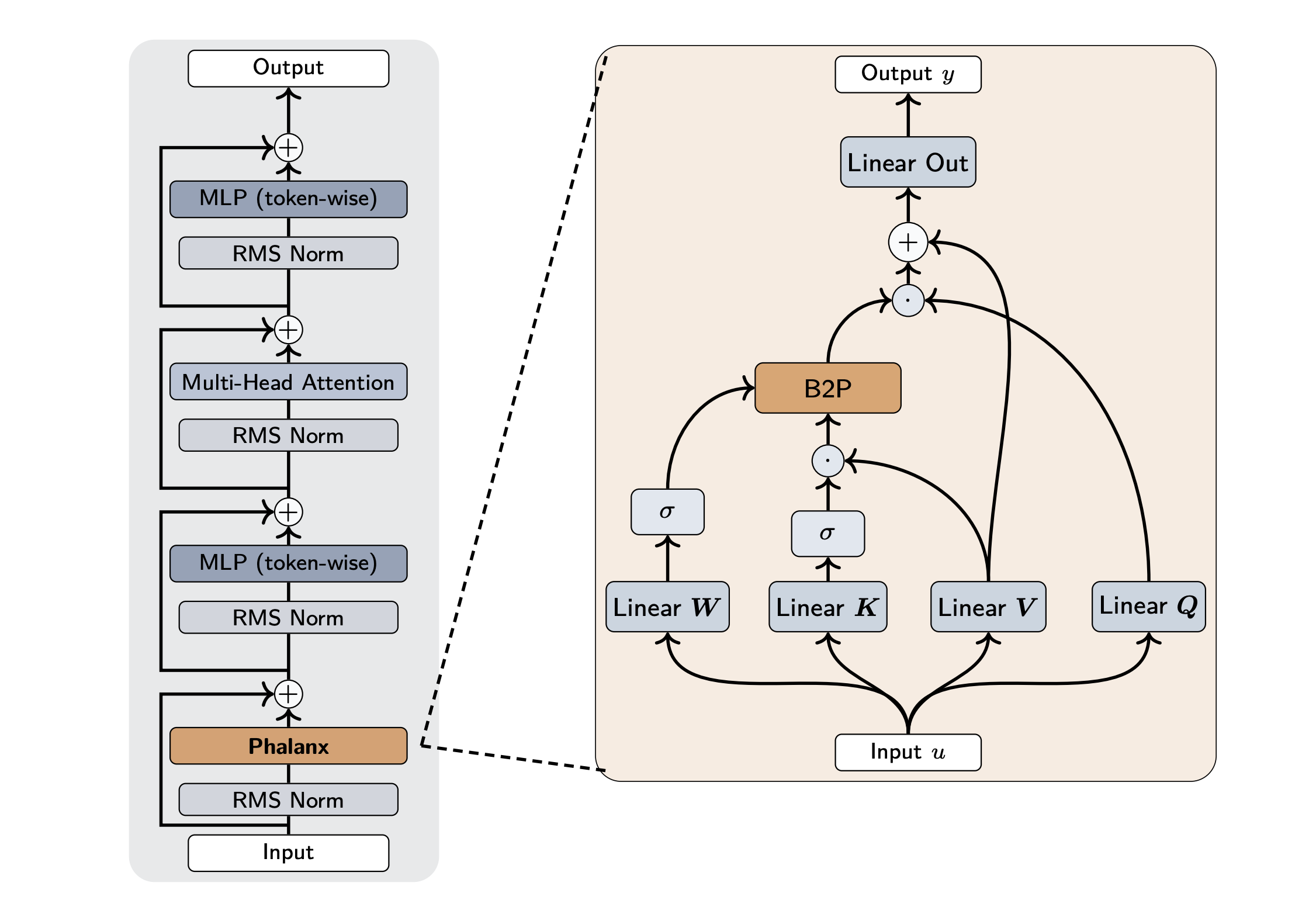
In particular, Phalanx is an input-varying layer with pre-gating, post-gating, and linear layers for all featurizer projections. Phalanx uses Q and K sharing, tiling the same gate across the head dimension to improve throughput without loss of quality. At the core of Phalanx is a Sliding Window Recurrence (SWR), which enables efficient token mixing at the lowest level of the GPU hierarchy through a new B2P algorithm.

Hybrid Language Models and Windowed Operators

Hybridization in model architectures, i.e., combining attention with complementary operators, has emerged as a practical path to improving both training and inference efficiency without sacrificing quality [1, 2, 3, 6, 11, 12]. Early large-scale hybrid models demonstrated that mixing operators with distinct inductive biases can outperform attention-only models, a trend now seen across large foundation models such as StripedHyena 2, GPT-OSS, and Qwen3-Next, among others.

Windowed operators such as SWA [4] and Hyena-SE [5] create effective hybrid models by delegating long-range modeling to the other layers of the model. Windowed operators also achieve faster throughput across sequence lengths, unlike many subquadratic architectures. However, while global attention variants have received extensive study, comparatively little work has focused on improving local layers.

Recurrence-style layers, including variants of linear attention, are increasingly adopted in hybrid models in production due to their strong language modeling performance [6, 8, 9, 10]. Yet the exponentially decaying bands characteristic of most linear recurrences, and the associated cost of computing long but weak interactions, make them natural candidates for adaptation into a windowed mixer.

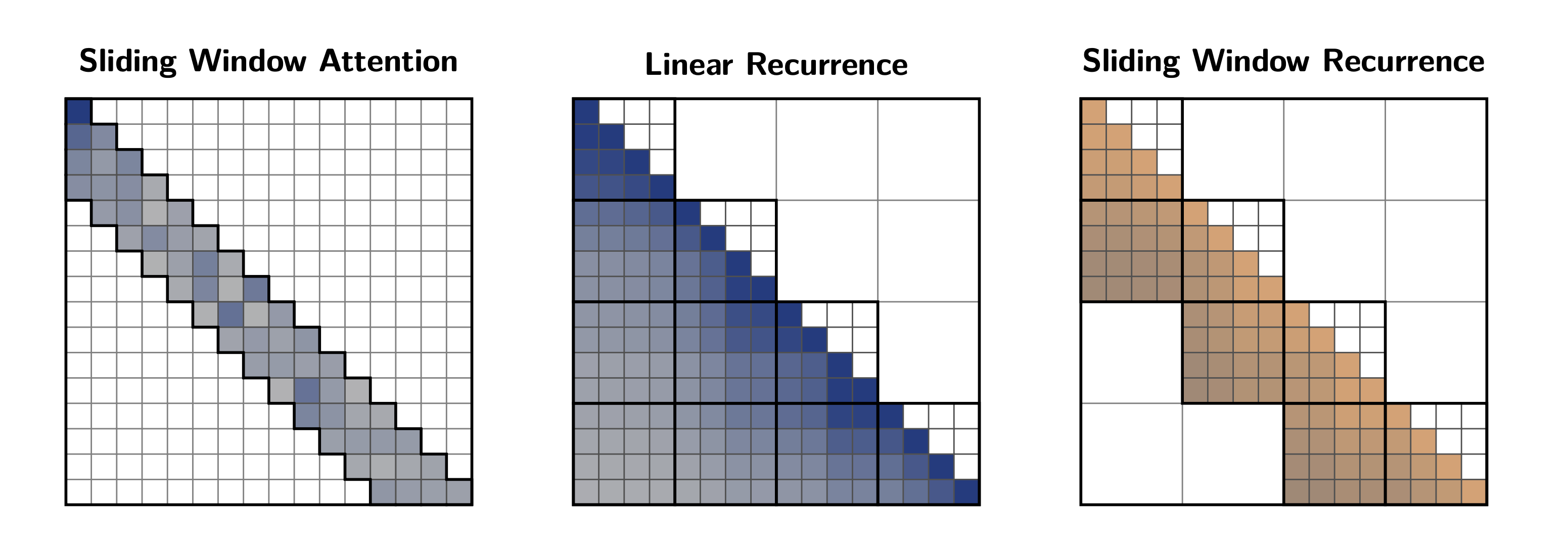
We therefore introduce Sliding Window Recurrences (SWR), which truncate the classical recurrence operator to act as an efficient local mixer. Naïve truncation, however, does not automatically yield efficiency on real hardware. Our work focuses on reducing data movement across the GPU memory hierarchy, leading to a new formulation of SWR that maximizes data locality and throughput.

The Hierarchical View

Data movement cost dominates computation by orders of magnitude. Each level of the GPU’s hierarchy (registers, shared memory, HBM) imposes distinct latency, bandwidth, and capacity constraints. Algorithmic design must explicitly account for this hierarchy to achieve true efficiency.

Flat algorithms operate at a single global indexing scale. In contrast, hierarchical algorithms use multiscale indexing schemes that align with the GPU memory hierarchy. This enables clean separation between short-range and long-range interactions, allowing different algorithms to operate at each scale and drastically reducing the cost of higher-level data movement.

A uniform window for SWR would result in a flat operator with poor locality. Instead, we introduce jagged bands that align naturally with GPU warp topology, enabling communication only between neighboring data. This yields a 1-to-1 mapping between algorithm structure and GPU layout, prescribing tile sizes, carry paths, and communication scope. Here, we focus on jagged SWR with block sizes of 16, directly mapping each block to a GPU warp to maximize data locality and throughput.

Our Proposed Block Two-Pass Algorithm

To understand how Phalanx achieves its speed, we need to look at how linear recurrences work mathematically. A linear recurrence updates its state one step at a time:

$$x_i = a_i x_{i-1} + u_i. \qquad (u_i: \text{inputs},~x_i:\text{states},~a_i:\text{coefficients})$$

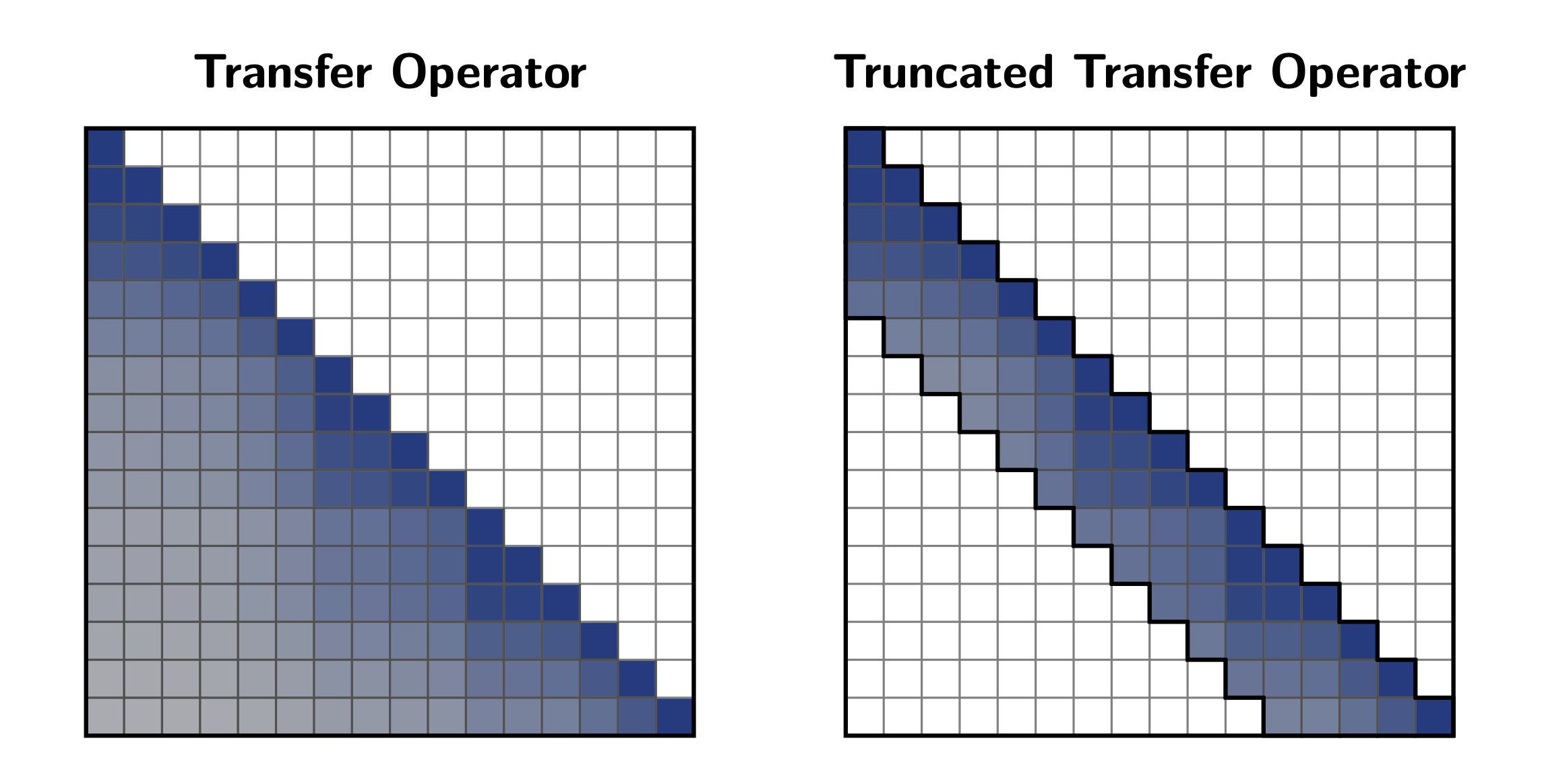
If we stack the whole sequence this step-by-step rule is exactly the same as applying a linear transformation to the inputs. This transformation can be represented as a matrix: the transfer operator. You can think of it as the recurrence equivalent of an attention matrix: it encodes the linear contribution of each input to the output.

The transfer operator has a special structure: it is lower triangular, output states only depend linearly on past inputs, and its values decay as you move away from the diagonal. In other words, distant inputs have exponentially weaker influence on the current state. This decay pattern motivates introducing a “locality prior”: by truncating this operator to a given band (window), cutting off the tail where influences are already negligible.

Breaking into two scales

We can decompose this full transfer operator into two separate transformations happening at different time scales

Full Recurrence = Local Recurrences (fast) + Global Recurrence (slow)

More precisely, imagine dividing your input sequence into chunks. The hierarchical decomposition is:

1. Local recurrences: within each chunk, run independent recurrences in parallel; these capture local interactions.
2. Global recurrence: At the chunk boundaries, run a coarser recurrence that integrates information across chunks; this handles long-range dependencies.

This corresponds to a matrix factorization where the block-diagonal part handles local computation, and a low-rank correction term handles communication between blocks.

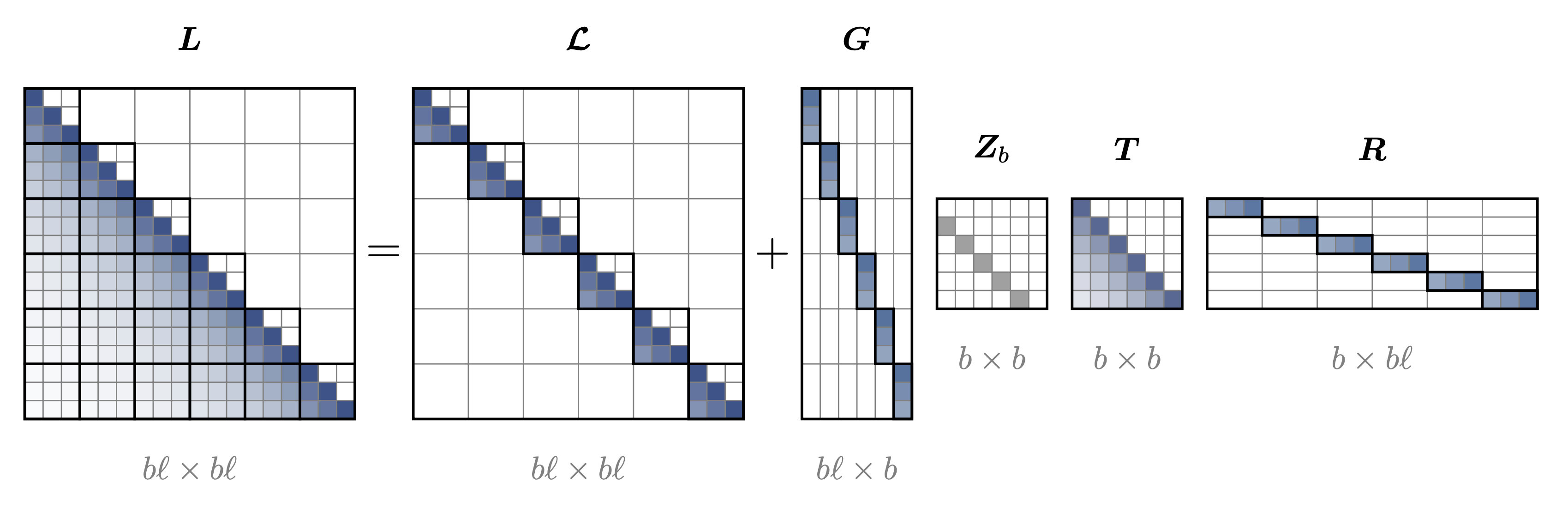
Note however that while the global recurrence is smaller than the original one, it happens at the more expensive communication level.

This is where SWRs come in. We truncate the decomposition to a bare minimum: we keep only the communication between adjacent blocks and drop the global recurrence entirely.

Think of it like this:

• Before truncation: block $i$ depends on all previous blocks, requiring (causal) global communication
• After truncation: block $i$ only receives information from block $i-1$, its immediate neighbor.

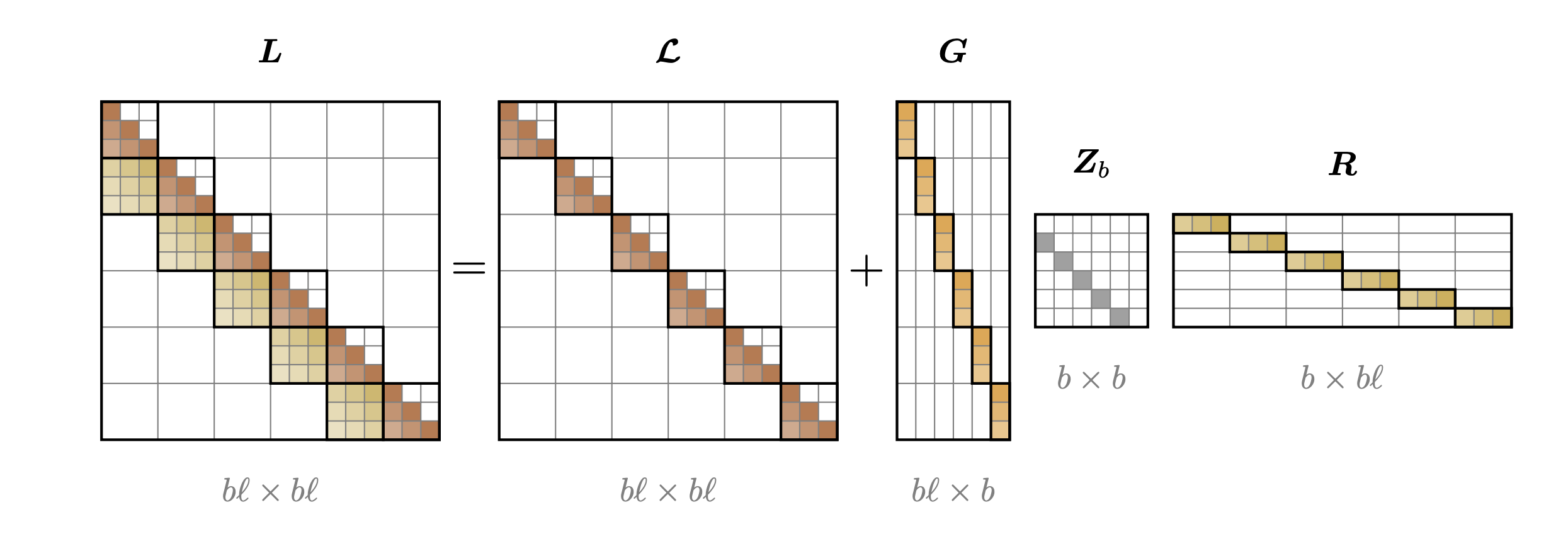
This jagged pattern, where each block depends only on its predecessor, is what enables the Block Two-Pass (B2P) algorithm to achieve constant depth and local communication. The first pass computes local recurrences in parallel, the second pass performs a simple neighbor update also in parallel, and we’re done.

GPU implementation

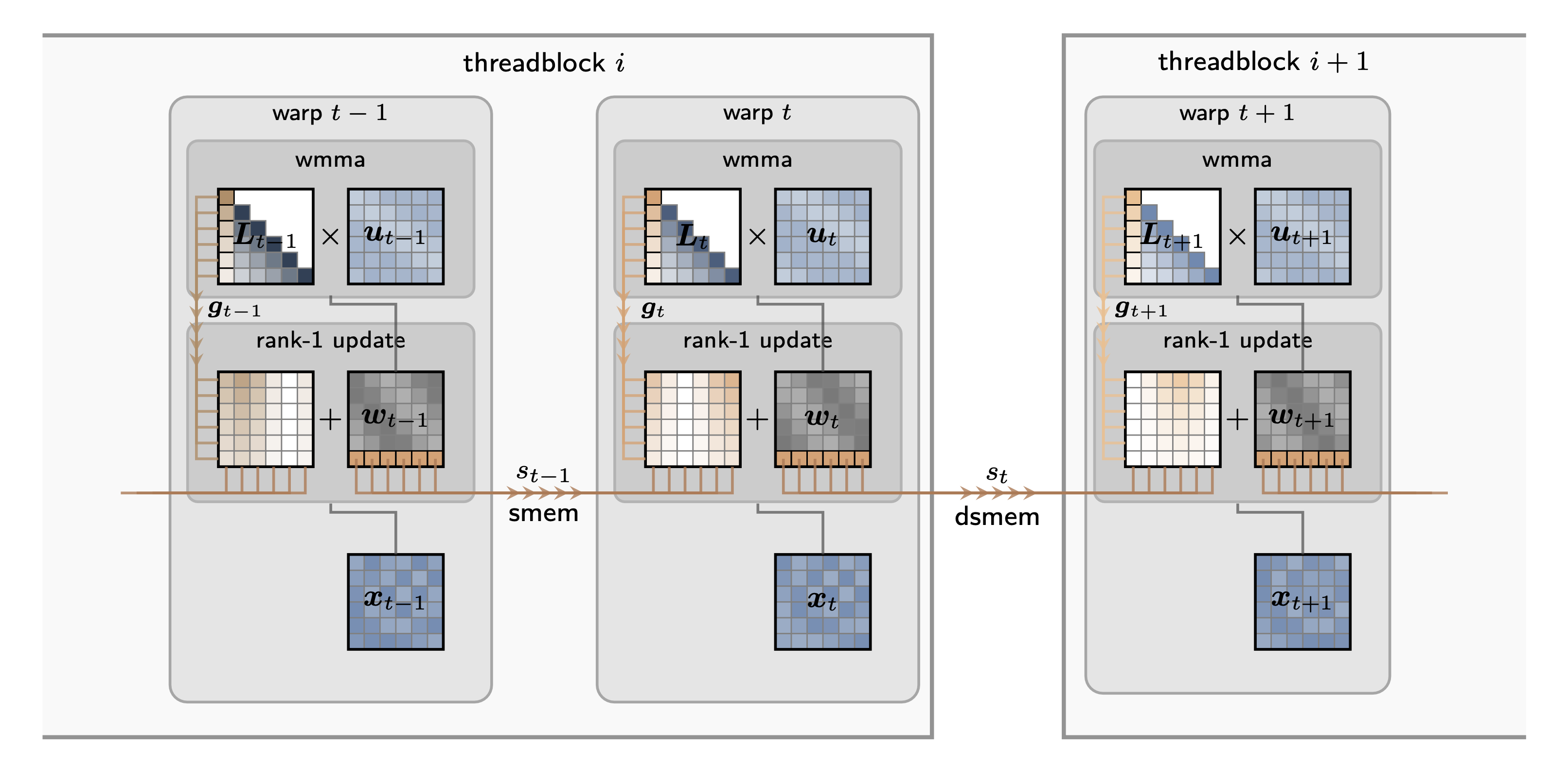
To map directly to hardware (here, NVIDIA H100s), we use block size of 16 such that each local computation fits in on a single warp. The B2P kernel has two stages:

Pass I – Local Recurrence: Within each warp, we compute the local recurrences (the independent chunks) using dense matrix multiplication primitives (warp matrix multiply accumulate) executed directly by the GPU’s systolic arrays. This fully utilizes the fast on-chip memory and compute pipelines. Weight sharing across head features maximizes throughput at this stage.

Pass II – Neighbor Update: We collect the final state (the carrier) from the immediately preceding warp and broadcast it through a rank-1 update to the current warp. Just like in the first pass, this update is done in parallel. Compared to global recurrences (e.g. Mamba, GLA, DeltaNets etc.), this drastically reduces communication since data flows only between neighboring warps. Using the B2P algorithm and kernel, we realize the data locality-first design of Phalanx, enabling us to train more efficient hybrid models.

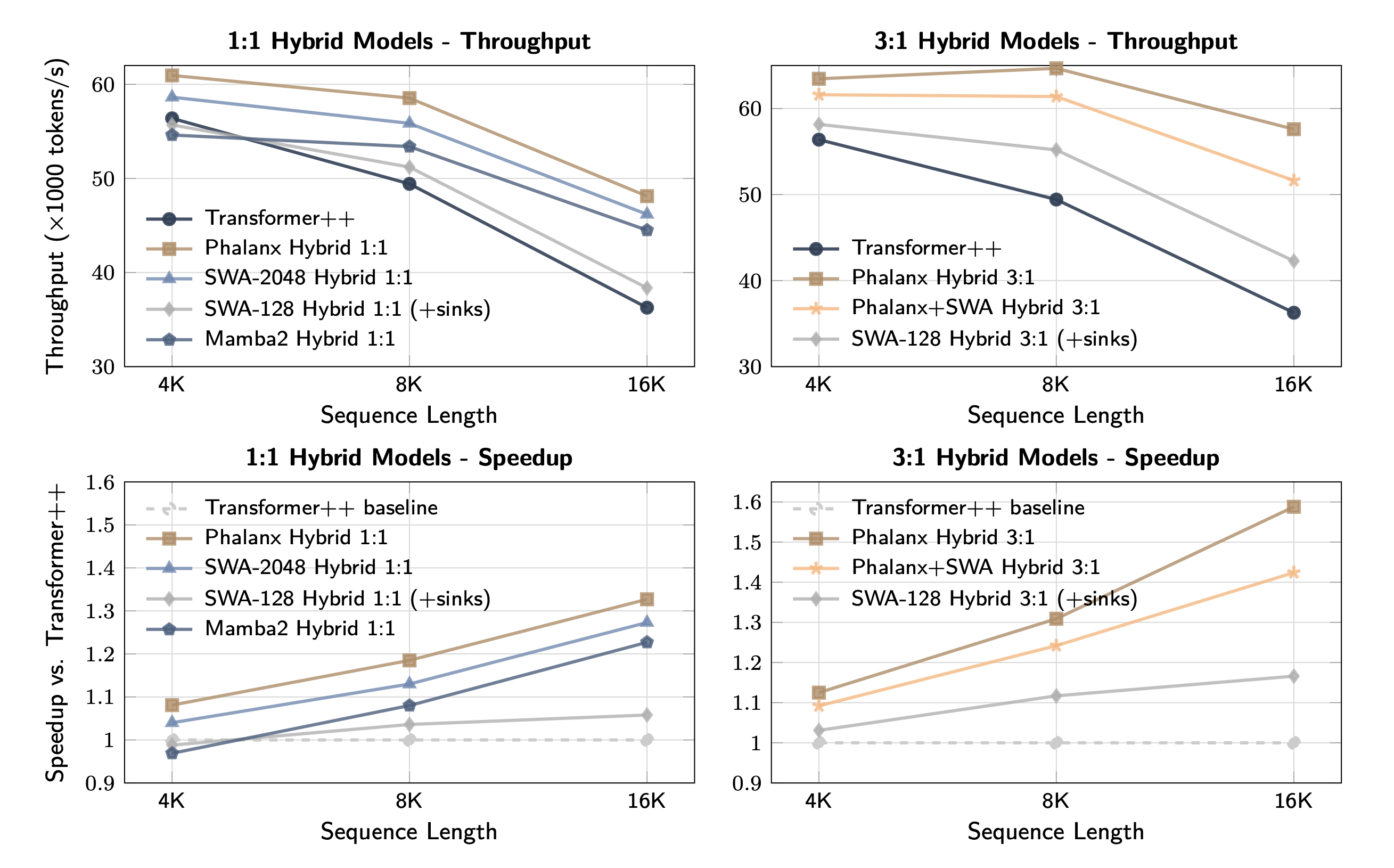
Results

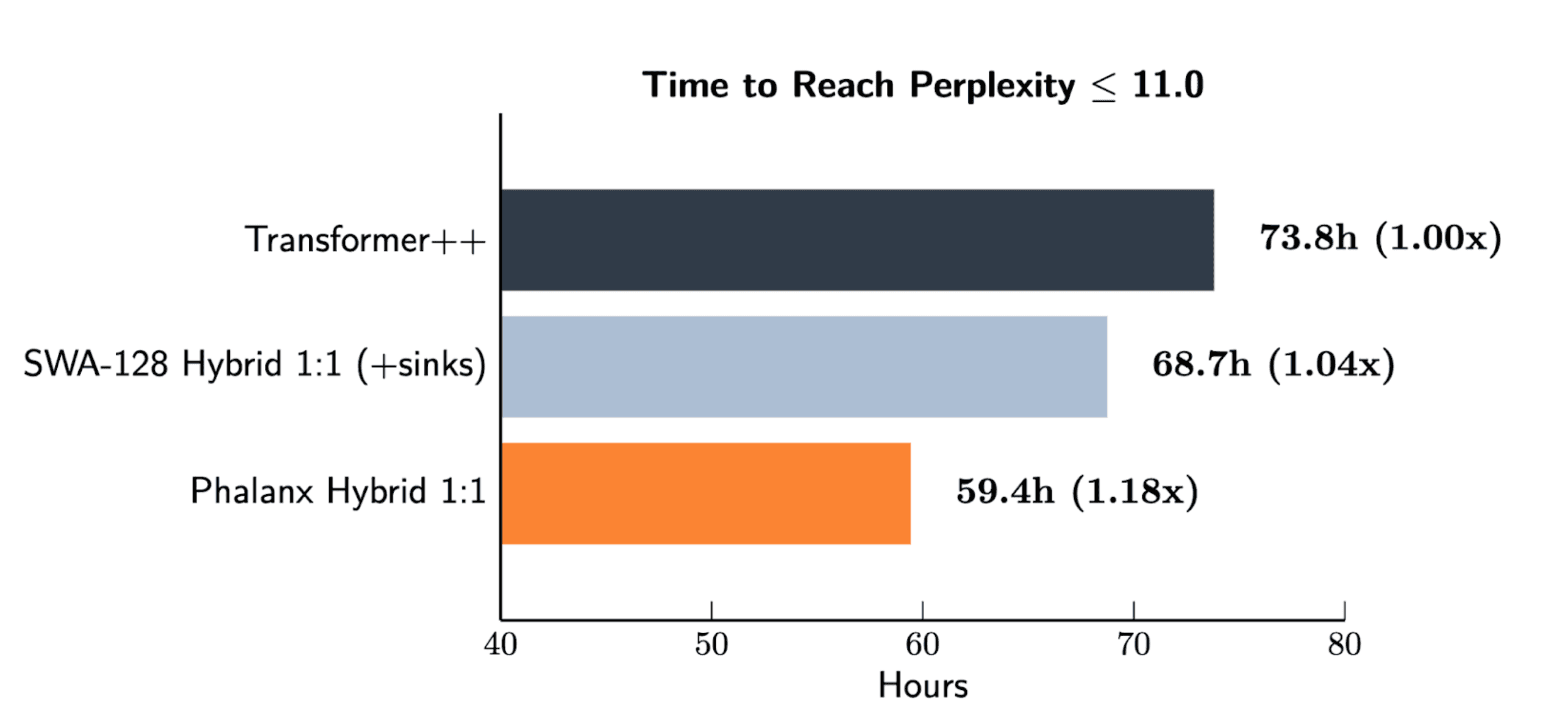
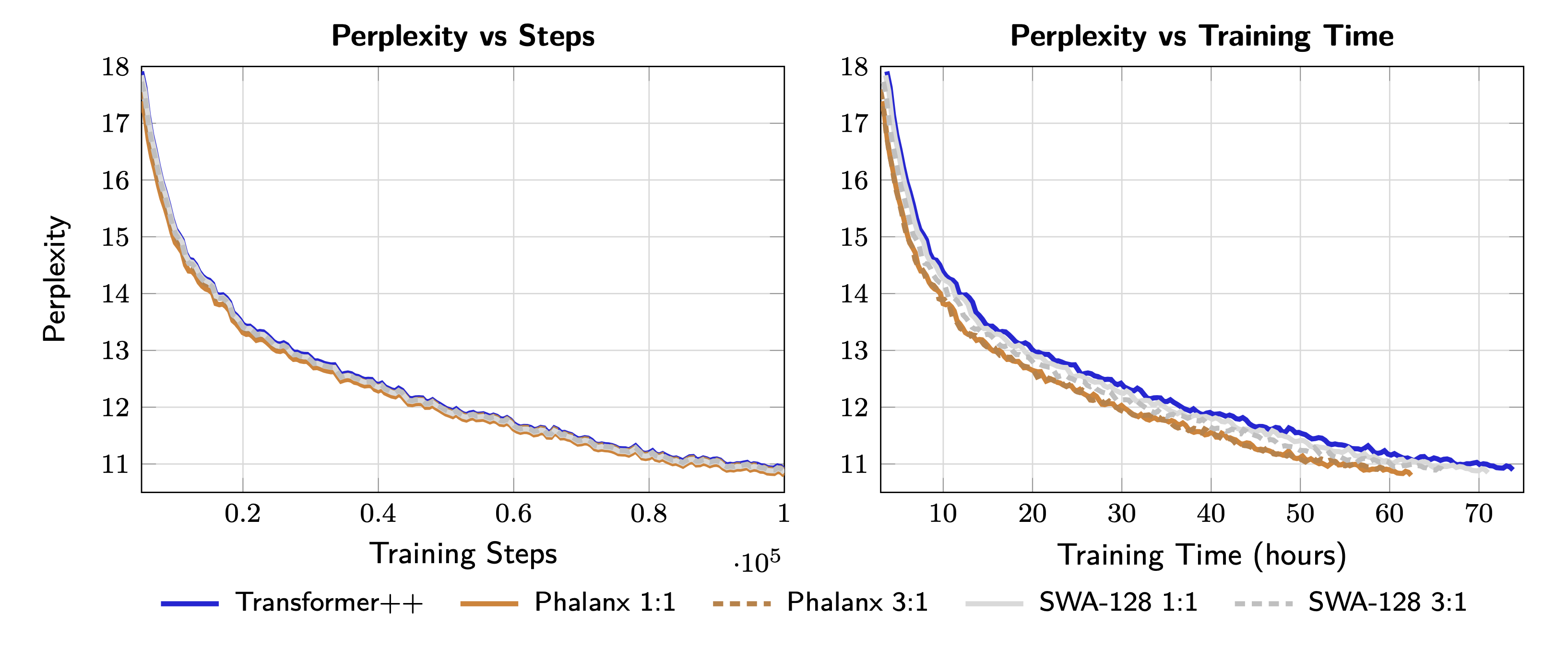
At 1B parameters and 8K context, Phalanx hybrids train up to 40% faster than Attention or SWA hybrid baselines while matching perplexity.

Phalanx hybrids maintain or exceed quality (FineWeb-Edu, 100 billion tokens):

Conclusion

By truncating long-range communication and exploiting hierarchy, Phalanx makes Sliding Window Recurrences (SWRs) a simple, fast, practical building block for hybrid models.

Phalanx is one example of how we approach the co-design of systems, architectures and numerics to unlock scaling on scientific data.

We're hiring → join us

References

[1] Michael Poli, Armin W Thomas, Eric Nguyen, Pragaash Ponnusamy, Björn Deiseroth, Kristian Kersting, Taiji Suzuki, Brian Hie, Stefano Ermon, Christopher Ré, et al. Mechanistic design and scaling of hybrid architectures. arXiv preprint arXiv:2403.17844, 2024.

[2] Dustin Wang, Rui-Jie Zhu, Steven Abreu, Yong Shan, Taylor Kergan, Yuqi Pan, Yuhong Chou, Zheng Li, Ge Zhang, Wenhao Huang, et al. A systematic analysis of hybrid linear attention. arXiv preprint arXiv:2507.06457, 2025b

[3] Arora, Simran, et al. "Simple linear attention language models balance the recall-throughput tradeoff." arXiv preprint arXiv:2402.18668 (2024).

[4] Iz Beltagy, Matthew E Peters, and Arman Cohan. Longformer: The long-document transformer. arXiv preprint arXiv:2004.05150, 2020

[5] Jerome Ku, Eric Nguyen, David W Romero, Garyk Brixi, Brandon Yang, Anton Vorontsov, Ali Taghibakhshi, Amy X Lu, Dave P Burke, Greg Brockman, et al. Systems and algorithms for convolutional multi-hybrid language models at scale. arXiv preprint arXiv:2503.01868, 2025

[6] Qwen Team, "Qwen3-Next: Towards Ultimate Training & Inference Efficiency," Qwen Blog, Sep. 10, 2025. [Online]. Available: https://qwen.ai/blog?id=4074cca80393150c248e508aa62983f9cb7d27cd&from=research.latest-advancements-list. [Accessed: Oct. 13, 2025].

[7] Yang, Songlin, et al. "Parallelizing linear transformers with the delta rule over sequence length." Advances in neural information processing systems 37 (2024): 115491-115522.

[8] Songlin Yang, Bailin Wang, Yikang Shen, Rameswar Panda, and Yoon Kim. Gated linear attention transformers with hardware-efficient training. arXiv preprint arXiv:2312.06635, 2023.

[9] Tri Dao and Albert Gu. Transformers are ssms: Generalized models and efficient algorithms through structured state space duality. arXiv preprint arXiv:2405.21060, 2024.

[10] S. Agarwal et al., "gpt-oss-120b & gpt-oss-20b model card," arXiv preprint arXiv:2508.10925, 2025.

[11] Brown, Tom, et al. "Language models are few-shot learners." Advances in neural information processing systems 33 (2020): 1877-1901.

[12] Fu, Daniel Y., et al. "Hungry hungry hippos: Towards language modeling with state space models." arXiv preprint arXiv:2212.14052 (2022).

Team

Garyk Brixi, Dragos Secrieru, Stefano Massaroli, Federico Berto, Alessandro Moro, Jerome Ku, Eric Nguyen, Armin W. Thomas, Michael Poli